© Tobias Thelen (www.tobiasthelen.de)
Diese HTML-Seiten sind eine Ausarbeitungmeines Referates über das Gefangenendilemma im besonderen und Spieltheorie im allgemeinen, das ich im Sommersemester 1997 im Seminar "Conflicts in AI" bei Prof. Dr. Rollinger gehalten habe. Es basierte auf dem Artikel "Random Strategies in a Two Levels Iterated Prisoner's Dilemma: How to Avoid Conflicts" von Jean-Paul Delahaye und Philippe Mathieu, ging aber in den Grundlagen weiter zurück und war eher geeignet, einen Überblick über das Gefangenendilemma insgesamt zu geben, als Spezialfragen tiefergehend zu behandeln, wie der Originalartikel es andeutet.
Bereichert werden die Seiten durch Ergebnisse von Experimenten, die ich selbst mit Studierenden der Einführungskurse "Programmieren für CL/KI I: Lisp" in den letzten 2 Jahren durchgeführt habe. Die dort als Lisp-Programme entwickelten Strategien stehen hier zum Mitnehmen zur Verfügung.
Generalisierend kann gesagt werden, daß die Spieltheorie interaktive Strategien von Individuen untersucht, die entgegengesetzte oder konfligierende Interessen haben. Das beschränkt sich keineswegs auf "Spiele" im engeren Sinne, jedoch kommen in künstlich herbeigeführten, spielähnlichen Situationen die zu untersuchenden Merkmale besonders deutlich und unverfälscht zum Tragen.
Eine sehr einfache und beliebte Klasse von Spielen sind dabei die Zwei-Personen-Spiele: Es gibt zwei Parteien, die sich gegenüberstehen und von nichts anderem als dem Verhalten des Gegners und ihren eigenen Zielen in ihren Entscheidungen beeinflußt werden. Ein weitere Beschränkung dazu sind Zwei-Personen-Nullsummenspiele, bei denen der eine Gegner gewinnt, was der andere verliert. In diesem Fall ist Kooperation ausgeschlossen, da nur einer von beiden gewinnen kann und somit der andere verlieren muß.
Die Spieltheorie untersucht Fragen der Interaktivität: Wie beeinflußt die Möglichkeit zur Kommunikation das Verhalten? Wie weit kann Kommunikation reduziert werden? Beim Schach ist es problemlos möglich, die Stellung der Figuren auf dem Brett als einzige Kommunikationsform zuzulassen, wie es etwa radikal beim Spielen mit einem Schachkomputer oder beim Briefschach passiert. Die einzige Form der Kommunikation beim Schach ist also das Mitteilen des nächsten Zuges. Die dahinterliegende Strategie, die kurz- und mittelfristig verfolgten Ziele werden nicht mitgeteilt (dann wäre wohl auch der Reiz des Spiels für menschliche Spieler verloren, obwohl es Situationen geben kann, in denen es sinnvoll ist, mit dem Gegner das laufende Spiel zu analysieren, z.B. in Lern- und Trainingssituationen, in denen der Wille zum Sieg nicht zwangsläufig fehlen muß). Wie sieht es hingegen bei Nicht-Nullsummen-Spielen aus, bei denen also die Spieler eventuell durch Kooperation oder sonstiges Zusammenfallen bestimmter Zugkombinationen gemeinsam Kapital schlagen, oder den Gewinn über den Verlust des Gegners hinaus steigern können? Kommunikation erhält dann eine entscheidende Bedeutung: Je mehr ich über die Absichten des Gegners weiß, desto höher wird mein Gewinn sein.
Im vorigen Absatz war von "Absichten" und "kurz- und mittelfristigen Zielen" die Rede. Ein exakterer Begriff für diesen Zweck ist der der "Strategie". Ein Strategie oder Entscheidungsregel ist eine exakte Spezifikation dessen, was in jeder möglichen Situtation des Spiels zu tun ist, anhand einer Strategie kann für jede Spielsituation ein Nachfolgezug angegeben werden. Die Entscheidungsregel muß nicht deterministisch sein, sondern kann Regeln enthalten, die mit Wahrscheinlichkeiten operieren, eine Strategie kann sogar vollständig zufallsbestimmt sein. Desweiteren basieren Entscheidungsregeln häufig auf der vorhandenen Spielsituation (die Frage, ob es erfolgreiche Strategien geben kann, die das nicht tun, wird später geklärt) oder auf einer Analyse der vorausgegangen Spielsituationen, entweder nur in diesem einen Spiel, oder in anderen, zu früheren Zeitpunkten durchgeführten Spielen.
Im Zusammenhang mit Strategien ist es ein Gegenstand der Spieltheorie, für bestimmte Situationen die Frage zu stellen: Welches Verhalten ist jetzt rational? Welche Strategie liefert optimale Ergebnisse? Allgemeiner wird nach generellen Eigenschaften erfolgreicher Strategien gefragt. Die Frage nach der Rationalität ist keine einfach zu beantwortende, insbesondere nicht, wenn nicht klar ist, ob die Spieler noch andere Ziele außerhalb des Spieles verfolgen (z.B. den Gegenüber nicht zu verärgern), oder ob Wissen über den Gegenüber mit verwendet wird. Beim Schach (oder auch beim Ausklügeln einer Fußballtaktik) kann solches Wissen ein große Rolle spielen. Wenn ich weiß, daß mein Gegner bestimmte Zugkombinationen bevorzugt einsetzt, kann ich davor besonders auf der Hut sein, wenn ich weiß, daß das gegnerische Team mit schnell vorgetragenen Kontern über die rechte Seite in der Vergangenheit häufig nicht zurecht gekommen ist, kann ich meinen Angriff darauf einstellen. Allerdings ergeben sich hier sehr schnell komplizierte Situationen der gegenseitigen Beeinflussung: Wenn der Gegner weiß (oder vermutet), daß ich über dieses Wissen verfüge, kann er seine Strategie modifizieren, was mich wiederum veranlassen könnte... Eine hübsche Veranschaulichung dieses Problems ist das "Paradoxon des überraschenden Besuchs": A kündigt B an, in der nächsten Woche überraschend zu Besuch zu kommen. B weiß: Wenn A bis Freitag noch nicht da war, muß er am Samstag kommen, das wäre dann aber nicht überraschend. Also scheidet der Samstag als Besuchstag aus, dasselbe gilt dann für den Freitag, den Donnerstag, den Mittwoch usw., bis B überzeugt ist, daß ein überraschender Besuch unmöglich ist. Schließlich kommt A völlig überraschend am Mittwoch zu Besuch.
Um solche Probleme bei der Betrachtung von Strategien auszuschließen, werden formalere Kunstspiele entwickelt, die in sehr engem Rahmen die Untersuchung reiner Strategien ermöglichen. Das Gefangenendilemma ist eines dieser Kunstspiele. Andererseits gibt es aber auch eine große Menge psychologischer und philosophischer Arbeiten über spieltheoretische Ansätze zur Untersuchung menschlicher Kommunikation und Interaktion, die außerhalb des Spieles liegende Einflüsse nicht ausschließen. In einem solchen Kontext wird dann z.B. nach den Umständen gefragt, in denen Menschen eine einmal gewählte Strategie ändern, d.h. zu der Überzeugung gelangt sind, daß eine andere Strategie vorteilhafter wäre. Das kann aus rationaler Überlegung, Verunsicherung oder auch schlicht Risikofreudigkeit geschehen.
In diesem Referat - und generell dem gesamten Seminar über die Behandlung von Konflikten zwischen Agenten mit Mitteln der Künstlichen Intelligenz - soll es aber eher um "berechenbare" Strategien gehen, die psychologische Vermutungen über den Gegner wenn nicht ausschließen, so doch in den Hintergrund stellen. So wird die Frage untersucht, ob es generelle Eigenschaften "erfolgreicher" Strategien gib, d.h. gibt es Merkmale von Entscheidungsregeln, die ein gutes Abschneiden garantieren oder wenigstens wahrscheinlich machen, unabhängig von den verwendeten Strategien der Gegner?
Untersuchungsgegenstand ist das Verhalten von "Individuen". Dieser Begriff ist sehr weit zu fassen: Klassischerweise handelt es sich um einzelne Menschen, doch kann auch das Verhalten von Gruppen von Menschen, bis hin zu Staaten spieltheoretisch untersucht werden. Abstraktere "Individuen" sind Firmen, die miteinander konkurrieren, die Abläufe auf Märkten aller Art sind ebenso bestimmt durch Konkurrenz, Interaktion, Gewinn und Verlust. Ein vierter Bereich sind Roboter, oder genauer Computerprogramme, die entweder mit realer Umwelt, oder aber eingeschränkten Spielsituationen konfrontiert werden.
Es soll mit Hilfe der Spieltheorie Verhalten, bzw. Verhaltensstrategien exakt beschrieben werden. Dazu werden Modelle aus der Mathematik, der Soziologie, den Wirtschaftswissenschaften, der Biologie und weiterer Disziplinen herangezogen. Ich beschränke mich hier auf die Erforschung von Konfliktsituationen anhand eines einfachen mathematischen Modells.
Die Geschichte der Spieltheorie als eigenständige Wissenschaft beginnt 1944 mit der Veröffentlichung von "Theory of Games and Economic Behavior" von John von Neumann und Oskar Morgenstern. Doch bereits vorher gab es weniger ausgearbeitet Ansätze, wie im babylonischen Talmud eine Vorschrift über die Aufteilung des Vermögens eines verstorbenen Mannes an seine Frauen, im 18. Jahrhundert über Kartenspiele, schließlich 1913 E. Zermelo: "Über eine Anwendung der Mengenlehre auf die Theorie des Schachspiels" und der Beweis des Maximin-Theorems von John von Neumann 1928.
In den 50er Jahren dieses Jahrhunderts haben Melvin Dresher
und Merrill Flood von der RAND Corporation als erste das
Gefangenendilemma experimentell benutzt, John Nash hat in
Arbeiten über Gleichgewichtszustände in 2-Personen-Spielen das
"Nash Equilibrium" entwickelt: DEFINITION: Nash
Equilibrium If there is a set of strategies with the property
that no player can benefit by changing her strategy while the
other players keep their strategies unchanged, then that
set of strategies and the corresponding payoffs constitute the
Nash Equilibrium.
Der Wirtschaftswissenschaftler Reinhard Selten hat 1965 das Buch "Spieltheoretische Behandlung eines Oligomodells mit Nachfrageträgheit" veröffentlich, und damit der Anwendung der Spieltheorie in den Wirtschaftswissenschaften neuen Auftrieb verschafft. Das wichtige Konzept der "Evolutionary Stable Strategy" wurde von John Maynard Smith 1974 eingführt und brachte die evolutionäre Spieltheorie einen großen Schritt vorwärts. Zur Popularisierung des Gefangenendilemmas und Implementationen von Strategien als sehr einfachen Computerprogrammen hat Robert Axelrod 1984 (deutsche Fassung 1988) mit der Veröffentlichung des Buches "The Evolution of Cooperation" beigetragen, auf dem große Teile dieses Referates beruhen.
Die endgültige wissenschaftliche Anerkennung der Spieltheorie erfolgte 1994 mit der Verleihung des Nobelpreises für Wirtschaftswissenschaften an John Nash, John C. Harsanyi und Reinhard Selten für ihre Beiträge zur Spieltheorie.
In den vorigen Abschnitten hat sich schon angedeutet, daß die Spieltheorie eine interdisziplinare Forschungsrichtung ist, die sowohl ihre Methoden und Modelle aus verschiedenen Wissenschaften bezieht, als auch mit ihren Ergebnissen in verschiedenen Disziplinen Beachtung findet.
Überall, wo Konkurrenz von "Individuen" um Ressourcen zu untersuchen ist, können spieltheoretische Untersuchungen eingesetzt werden, um entweder vorhandenes Verhalten zu erklären, oder aber verbesserte Strategien zu entwerfen. Ersteres geschieht besonders in denjenigen Wissenschaften, die über lange Zeit entstandene Situationen analysieren, wie etwa der Biologie oder der Soziologie. Im Tierreich lassen sich einige Beispiele finden, in denen sich eine dem gegenseitigen Vorteil dienende Kooperation entwickelt hat, auch in dem Sinne, daß eines der beteiligten Tiere "Vorleistungen" erbringt, die dann später "belohnt" werden. Ein Beispiel aus der Wirtschaftswissenschaft ist die Preisgestaltung zweier konkurrierender Unternehmen: Wenn ein Unternehmen das Produkt zu einem geringeren Preis anbietet, wird es einen höheren Umsatz vorweisen können und (falls der Preis nicht zu niedrig war) einen höheren Gewinn erzielen. Gleichzeitig möchte es aber den Preis möglichst hoch halten, damit der Gewinn möglichst groß ausfällt. Dieses Beispiel wird bei der Vorstellung des Gefangenendilemmas genauer untersucht werden.
In der Künstlichen Intelligenz und der Erforschung von
"Artificial Life" sollen künstliche Agenten so
programmiert werden, daß sie in der (realen oder simulierten)
Umwelt "überleben" bzw. erfolgreich sein können. Auch
hier treten häufig Konkurrenzsituationen auf, in denen die
Agenten mit anderen Agenten oder realen Objekten um Resourcen
streiten. Schließlich werden bei modernen Computerspielen die
künstlichen Gegner mit Strategien ausgestattet, die den Eindruck
eines "echten" Gegners entstehen lassen. Dabei soll der
Gegner nicht unbesiegbar sein, in Echtzeit agieren und nicht zu
leicht zu durchschauende Muster der Aktionen aufweisen. Ein gutes
Beispiel sind die in den letzten Jahren sehr beliebt gewordenen
Echtzeit-Strategiespiele (Dune2, Command & Conquer, War
Craft), bei denen zwei konkurrierende "Stämme" oder
"Rassen" mit begrenzten Ressourcen Siedlungen und
Stützpunkte errichten und das Ziel verfolgen, das Gebiet des
Gegners durch Angriffe zu erobern.
Für Zwei-Personen-Nullsummen-Spiele liefert die Maximin-Strategie die optimale Lösung: Ich versuche, das Minimum der erreichbaren Punkte zu maximieren.. Ein Beispiel für die Berechnung der Lösung eines Zwei-Personen-Nullsummenspiels mit der Maximin-Strategie findet sich weiter unten. Bei Nicht-Nullsummen-Spielen ist das nicht immer möglich. Es kann mehrere Lösungskonzepte geben, von denen keines per se "das richtige" ist. Im Anschluß an die Beschreibung des Gefangenendilemmas wird ein anderer Lösungsweg aufgezeigt, nämlich die "dominante Strategie" und das "dominante Strategien Gleichgewicht".
Das Gefangenendilemma ist das klassische Zwei-Personen-Nicht-Nullsummen-Spiel, das in seiner ursprünglichen oder einer abgewandelten Form auch noch 45 Jahre nach seiner Einführung ein wichtiger Bestandteil der Spieltheorie ist.
| Zwei Gefangene sind verdächtig, gemeinsam eine
Straftat begangen zu haben. Die Höchststrafe für das
Verbrechen beträgt 5 Jahre. Der Richter macht jedem der beiden folgendes Angebot: Wenn Du auspackst, und somit Deinen Partner belastest, kommst du ohne Strafe davon und er muß die vollen 5 Jahre absitzen. Wenn ihr beide schweigt, haben wir genügend Indizienbeweise, um euch für 2 Jahre einzusperren, wenn ihr beide gesteht, müßt ihr 4 Jahre eures Lebens hier verbringen. Die beiden Gefangenen haben keine Möglichkeit, sich über ihr Vorgehen abzustimmen. Wie werden sie sich entscheiden? |
Jeder der Gefangenen hat zwei Möglichkeiten: schweigen oder
gestehen, oder (aus Sicht des anderen Gefangenen) kooperieren
oder defektieren (cooperate/defect). Die Punktwerte für jede der
vier möglichen Zugkombinationen werden üblicherweise in einer
payoff-Matrix angegeben.
| A / B | schweigen | gestehen |
| schweigen | (-2,-2) | (-5,0) |
| gestehen | (0,-5) | (-4,-4) |
Tabelle 1: payoff-Matrix für das Gefangenendilemma
Tabelle 1 zeigt die Payoff-Matrix für die im Text beschriebene
Situation, dabei ist die Anzahl der im Gefängnis zu verbingenden
Jahre als negative Zahl eingetragen, eine höhere Punktzahl ist
also für den Gefangenen besser als eine niedrigere. Tabelle 2
zeigt die übliche Darstellung, bei der bei jedem Wert 5 addiert
wurde, was das Problem jedoch nicht verändert, sondern lediglich
durch das Rechnen mit positiven Punktzahlen etwas angenehmer ist.
Die vier Kombinationen werden (aus Sicht von Spieler A)
bezeichnet mit R (=reward) für beiderseitige Kooperation, P
(=punishment), falls beide defektieren. Die Versuchung T
(=temptation), den Gegner reinzulegen steht der Gefahr
gegenüber, hereingelegt zu werden (S=sucker).
| A / B | cooperate | defect |
| cooperate | R=(3,3) | S=(0,5) |
| defect | T=(5,0) | P=(1,1) |
Tabelle 2: payoff-Matrix für das Gefangenendilemma
Die konkret gewählten Werte für R, S, T und P sind ersetzbar, jedoch müssen folgende Bedingungen erfüllt sein:
D.h. die höchste Punktzahl gibt es für die Versuchung, den Gegner hereinzulegen, die Belohnung bei gegenseitiger Kooperation muß echt kleiner sein, sonst besteht (außer vielleicht der Schadenfreude) kein Anlaß, zu defektieren, d.h. zu gestehen. Desweiteren muß die Punktzahl für R größer sein als die für gegenseitiges defektieren, denn sonst bestünde keinerlei Anreiz zur Kooperation, also die Hoffnung, daß beide kooperieren und damit eine höhere Punktzahl bekommen, als wenn beide defektieren. Der niedrigste Wert muß schließlich vergeben werden, wenn der Spieler hereingelegt wird, damit das Gegenstück zur Versuchung, den Gegner hereinzulegen vorhanden ist. Die Punktzahl für T+S darf deshalb nicht größer oder gleich R sein, damit nicht abwechselndes Hereinlegen (bei Wiederholung des Spiels) attraktiver als gegenseitige Kooperation ist.
Wenn die payoff-Matrix gegen eine oder mehrere dieser Bedingungen verstößt, gelten die folgenden Betrachtungen über das Gefangenendilemma nicht mehr, es handelt sich dann um eine Variante, die am Ende dieses Textes beschrieben werden.
Es existieren eine Reihe von alternativen Formulierungen des
Gefangenendilemmas, in den Übungen zu "Programmieren für
CL/KI I: Lisp" wurde folgende gewählt:
In schwierigen Zeiten sollst Du auf dem Schwarzmarkt Waren
tauschen. Dazu sollen Du und Dein Tauschpartner zu einem
bestimmten Zeitpunkt an verschiedenen Stellen die Ware
hinterlegen. Natürlich ist Dein Gewinn am größten, wenn Du
nichts hinterlegst und dafür die gewünschte Ware bekommst. (Das
gleiche gilt aber leider auch für Deinen Partner). Du hast keine
Möglichkeit herauszubekommen, ob Dein Partner die Ware
hinterlegen wird oder nicht. Dieselbe Prozedur wiederholt sich
Woche für Woche, wobei Du natürlich das bisherige Verhalten
Deines Partners mit in Betracht ziehen solltest.
Dieses Szenario (das in ähnlicher Form bei Douglas Hofstadter im "Metamagicum" beschrieben ist), beinhaltet bereits eine ständige Wiederholung des Spiels. Das sogenannte "einfache Gefangenendilemma" hat eine eindeutige rationale Lösung, die es damit allerdings für weitere Untersuchungen uninteressant macht. Nach einer Begründung dieser rationalen Lösung wende ich mich deshalb dem "iterierten Gefangenendilemma" zu.
Jeder der beiden Gefangenen oder der beiden Schwarzmarkthändler will seinen Gewinn maximieren, d.h. ihn interessiert nicht, wieviele Punkte der Gegner bekommt, sondern nur sein eigenes Abschneiden.
Ausgehend von der Aktion des Gegners gibt es zwei Möglichkeiten:
Es ist also in jedem Fall besser, zu defektieren, unabhängig davon, was der Gegner tut (oder tun könnte, denn das Ergebnis zeigt sich ja erst, nachdem beide ihren Zug gemacht haben). Damit ergibt sich die unangenehme Situation, daß rationales Verhalten beider Spieler zu einem suboptimalen Ergebnis führt: Beide bekommen 1 Punkt, bei gegenseitiger Kooperation wären es aber 3 gewesen.
Die Spieler sind in ein "dominante-Strategien-Gleichgewicht" ("dominant strategy equilibrium") geraten. Der Beweis der Existenz eines solchen Gleichgewichtszustandes stellt die rationale Lösung eines Zwei-Personen-Nicht-Nullsummen-Spieles dar. Die Begriffe "dominante Strategie" und "dominante-Strategien Gleichgewicht" werden nach R.A. McCain ("Game Theory: An introductionary sketch") wie folgt definiert:
Definition "dominante Strategie":
Ein einzelner Spieler berechnet getrennt jede der
Strategiekombinationen, die auftreten können (eine Strategie ist
in diesem Fall das einmalige kooperieren oder nichtkooperieren)
und wählt jeweils aus seinen eigenen Strategien (=
Zugmöglichkeiten) diejenige, die für ihn den größten Gewinn
bringt. Wenn für jede der möglichen Kombinationen die gleiche
Strategie gewählt wird, wird diese Strategie für diesen Spieler
in diesem Spiel eine "dominante Strategie"
("dominant strategy") genannt.
Definition "dominante-Strategien-Gleichgewicht":
Falls in einem Spiel für jeden Spieler eine dominante Strategie
existiert und jeder Spieler seine dominante Strategie benutzt,
dann führt diese Kombination dominanter Strategien und ihrer
Punktzahlen zu einem "dominante-Strategien-Gleichgewicht"
("dominant strategy equilibrium").
Beim Gefangendilemma ist es für jeden Spieler die dominante
Strategie, zu gestehen, d.h. zu defektieren. Das Gleichgewicht
tritt ein, wenn beide Spieler dieser Strategie folgen.
Ändert sich dieses Gleichgewicht, wenn das Spiel wiederholt wird? Diese Frage soll zunächst für eine bekannte Anzahl von Runden untersucht werden, d.h. jeder Spieler weiß im voraus, welche Runde die letzte ist. In dieser letzten Runde gilt auf jeden Fall die oben erarbeitete dominante Strategie, denn die Möglichkeit der "Rache" seitens des anderen Spielers für ein mögliches Hereinlegen gibt es hier nicht mehr. In der letzen Runde werden also beide Spieler defektieren. Also gibt es auch in der vorletzten Runde keinen Grund, Vergeltung zu fürchten und somit keine Veranlassung von der dominanten Strategie abzuweichen. Analog zu dem oben beschriebenen "Paradoxon des unmöglichen Besuchs" ist bei einer bekannten Anzahl von Runden defektieren die rationalerweise zu wählende Strategie. Das führt bei n Runden zu einer Punktzahl von n*2 Punkten statt der bei beiderseitiger Kooperation möglichen Zahl von n*3 Punkten.
Defektieren ist die einzige rationale Strategie beim
einfachen Gefangenendilemma bzw. einer bekannten Anzahl von
Runden.
Ein einfaches Beispiel für ein Nullsummenspiel, bei dem die Maximin-Strategie anwendbar ist, ist der Wettbewerb zwischen zwei Konkurrenten (in diesem Fall Mineralwasseranbieter), die vor der Entscheidung stehen, ihr Produkt für $1 oder $2 anzubieten. Falls der Preis $1 ist, werden auf dem Markt insgesamt 10.000 Flaschen verkauft, für $2 werden insgesamt 5.000 Flaschen verkauft. Die festen Kosten jeder Firma betragen $5.000. Falls beide Firmen ihr Produkt zum gleichen Preis anbieten, verkauft jeder die gleiche Anzahl Flaschen, d.h. der Gewinn wird geteilt und reicht dann für jede Firma aus, ihre Kosten zu decken. Wenn aber einer der beiden Konkurrenten zu einem geringeren Preis verkauft, werden alle Flaschen von ihm abgenommen und der andere Anbieter geht leer aus. In diesem Fall gewinnt die eine Firma $5.000, die andere verliert $5.000. Tabelle 3 zeigt die Payoff-Matrix für dieses Zwei-Personen-Nullsummenspiel.
| Perrier / Apollinaris | $1 | $2 |
| $1 | (0,0) | (+5000,-50000) |
| $2 | (-5000,+5000) | (0,0) |
Tabelle 3: payoff-Matrix für das Mineralwasserproblem
Aus der Maximin-Strategie folgt die Überlegung, daß ich bei einem Preis von $2 ein Minimum von -5000$ erzielen kann, bei einem Preis von $1 aber nur ein Minimum von $0. Also ist nach Maximin ein Preis von $1 vorzuziehen.
Das ist auch für jeden der beiden Spieler die dominante Strategie: Den Preis auf $1 zu senken, um entweder einen Verlust von $5.000 zu verhindern (falls der Gegner den Preis auf $1 festsetzt), oder einen Profit von $5.000 zu erzielen (falls der Gegner $2 nimmt). Spielen beide Spieler ihre dominante Strategie, liegt wieder ein dominante-Strategien-Gleichgewicht vor.
Ein komplexeres und etwas realistischeres Beispiel zeigt Tabelle 4. Zwei Firmen haben nun die Wahl ihr Produkt zum Preis von p=1, 2 oder 3 Einheiten anzubieten. Die Payoff-Werte sind Gewinne nach Abzug aller anfallenden Kosten. Hier ist die grundsätzliche Idee, daß diejenige Firma, die einen geringeren Preis verlangt, einen höheren Absatz erzielt und in Grenzen auch einen höheren Profit als ein Mitbewerber, der einen höheren Preis verlangt.
| Firma A | Firma B |
|||
| p=1 | p=2 | p=3 | ||
| p=1 | (0,0) | (50,-10) | (40,-20) | |
| p=2 | (-10,50) | (20,20) | (90,10) | |
| p=3 | (-20,40) | (10,90) | (50,50) | |
Tabelle 4: Angebot eines Produktes von zwei Firmen zu drei verschiedenen Preisen
Offensichtlich ist dies kein Nullsummen-Spiel, die Profite können addiert 100, 40, 20 oder 0 ergeben, abhängig von den gewählten Strategien. Die Maximin-Strategie liefert hier kein sinnvolles Ergebnis, das wäre in jedem der möglichen Fälle ein Preis von p=1. Falls aber Firma B p=3 wählt, ist die beste Wahl für Firma A p=2, in den beiden anderen Fällen p=1. Keine der beiden Strategien ist dominant, es gibt also auch kein "dominante-Strategien-Gleichgewicht".
Ein anderes, allgemeineres Gleichgewichtskonzept ist das eingangs schon erwähnte Nash Equilibrium, das als Lösungskonzept in der Spieltheorie sehr weit verbreitet ist. Die Definition lautet nach McCain:
DEFINITION: Nash Equilibrium If there is a set of strategies with the property that no player can benefit by changing her strategy while the other players keep their strategies unchanged, then that set of strategies and the corresponding payoffs constitute the Nash Equilibrium.
Diese Definition läßt sich auf das vorige Beispiel anwenden, indem Strategiepaare betrachtet werden. Wenn beide Parteien p=3 "spielen", ist dies kein Nash-Equilibrium, denn jeder könnte dadurch profitieren, den Preis zu senken, wenn der Gegner bei seiner Wahl bleibt. Das gleiche gilt z.B. für das Paar (p=2, p=3), in diesem Fall kann B dadurch, daß der Preis auf p=2 gesenkt wird, profitieren. Auf diese Weise können alle Paare von Strategien, bis auf (p=1,p=1) als Nash Equilibrium ausgeschlossen werden.
Das Nash-Equilibirum im vorliegenden Beispiel ist ein Gleichgewichtszustand mit niedrigem Preis und keinem Profit. Viele Wirtschaftswissenschaftler behaupten, daß dieses Resultat eine zutreffende Beschreibung realer Märkte mit hohem Wettbewerb darstellt, obwohl das Beispiel immer noch eine starke Vereinfachung und Abstrahierung ist.
Bei nochmaliger Betrachtung der vorangegangenen Beispiele (Mineralwasser und Gefangenendilemma) zeigt sich, daß die dort festgestellten Gleichgewichtszustände auch Nash Equilibren sind. In der Tat sind die Konzepte aufeinander aufbauend: Jede Maximin-Lösung ist auch ein "dominante-Strategien-Gleichgewicht" und ein Nash Equilibirum, jedes "dominate Strategien Gleichgewicht" stellt gleichzeitig ein Nash Equilibrium dar.
Im weiteren beschäftige ich mich mit dem iterierten Gefangenendilemma und der Frage, wie trotz eines "ungünstigen" Gleichgewichtszustandes Kooperation entstehen kann. Es gibt noch weitere Definitionen von Gleichgewichtszuständen wie z.B. mehrfachen Nash Equilibrien und dazugehörige Analysen. Für diesen Themenkomplex verweise ich auf weiterführende Literatur wie z.B. McCain.
Das einfache Gefangenendilemma (und auch ein wiederholtes mit bekannter Anzahl von Zügen) besitzt einen Gleichgewichtszustand, der ein suboptimales Ergebnis für beide Spieler hervorbringt. Dadurch, daß beide immer defektieren, entgeht ihnen die Belohung für gemeinsames Kooperieren. Bezogen auf die erste Veranschaulichung des Gefangenendilemmas (gestehen oder schweigen) ist eine Wiederholung mit einer unbekannten Anzahl an Spielzügen unwahrscheinlich, beim Schwarzmarktszenario hingegen ist ein erneutes Tauschen in jeder Woche problemlos vorstellbar.
Wenn die Existenz eines "negativen" Gleichgewichtszustandes und somit der rationalen Begründbarkeit einer Strategie, die dem eigentlichen Zweck des Unternehmens zuwiderläuft, das Handeln der Teilnehmer bestimmen würde, dann würde es niemals zu einem erfolgreichen Tausch, d.h. einer beiderseitigen Kooperation kommen. In ähnlichen, realen Situationen, an denen Menschen als Handelnde beteiligt sind, kommt es aber sehr häufig zu Kooperationen. Das kann verschiedene Gründe haben:
Im Rahmen einer formalen Betrachtung ist vor allem der letzte Grund zu untersuchen. Das Thema des Seminars "Conflicts in AI" zielt darauf ab, allgemeine Verhaltensweisen, d.h. Handlungsstrategien, für künstliche Agenten in Konfliktsituationen zu untersuchen und zu bewerten. Der Agent tritt "gegen" eine Umwelt an, er muß versuchen seinen eigenen Erfolg zu maximieren, wobei die Strategien und Ziele der anderen beteiligten Agenten unbekannt sind. Je kleiner die Menge der zu berücksichtigenden Faktoren ist, desto einfacher und erfolgversprechender ist es, formale Handlungsanweisungen zu finden. D.h., wenn es möglich ist, auf die Explizierung spezifischer unscharfer Faktoren, wie ethischer Konventionen zu verzichten, ist dies ein Gewinn für die Programmierung erfolgreicher künstlicher Agenten. Im folgenden wird ein formaler Rahmen beschrieben, der experimentelles Testen verschiedener Strategien ermöglicht und ihre Komplexität nicht beschränkt.
Die zu untersuchenden Fragen sind:
Robert Axelrod hat 1981 einen Aufruf an Programmierer, Experten und Laien der Spieltheorie und alle anderen Interessierten verfasst, mögliche Strategien in einem iterierten Gefangenendilemma als Computerprogramme zu implementieren und sie gegeneinander in einem Turnier antreten zu lassen.
Eine Strategie in Axelrods Sinn war dabei eine Funktion, die, gegeben die Liste der bisherigen Spielzüge, den nächsten zu spielenden Zug eines Spielers ausgibt. Es gibt keine weiteren Informationen über die Spielsituation, insbesondere keine Informationen über die Identität, d.h. die Strategie des Gegners. Allerdings ist es jeder Funktion erlaubt, eine beliebige Menge von eigenen Variablen zu speichern.
In den Übungen zur Vorlesung "Programmieren für CL/KI I: Lisp" haben wir Erstsemestern, die in der Regel nicht mit dem Gefangenendilemma vertraut waren, genau diese Aufgabe gestellt und eine Experimentierumgebung in Lisp zusammen mit einigen Beispielstrategien zur Verfügung gestellt. (Lispcode)
Was ist in einem solchen Szenario eine erfolgreiche Strategie? Auf den ersten Blick denkt der Betrachter, wie ich in verschiedenen Situationen einschließlich des Selbstversuchs fetstellen konnte, an eine relativ komplizierte Strategie, die dadurch erfolgreich ist, daß die die Strategie des Gegners herauszufinden versucht. Ziel kann dann sein, den Gegner möglichst geschickt auszunutzen, d.h. so, daß er es nicht "merkt", oder keine Chance bekommt, "zurückzuschlagen", oder aber den Gegner zur Kooperation zu bewegen. Eine Strategie kann also bestrebt sein, entweder möglichst oft "T" (= Temptation) zu erlangen und zu defektieren, wenn der Gegner kooperiert, oder aber "R" (= Reward) und mit dem Gegner zusammen zu kooperieren. Von den vier möglichen Ausgängen einer Runde gibt es zwei, bei denen ein Spieler im Vorteil ist, und zwei, bei denen beide Spieler den gleichen Gewinn erzielen. Es kann nicht erwartet werden, den Gegner auf Dauer auszunutzen, d.h. auf Dauer T erzielen zu können. Abgesehen von sehr "dummen" Strategien, die nicht die Möglichkeit nutzen, vorangegangene Spielzüge mitzuberücksichtigen, wird jede Strategie in diesem Fall ebenfalls defektieren und beide Spieler erhalten P (=Punishment) Punkte.
So lassen sich mögliche Strategien grob in drei Gruppen einteilen:
| kooperativ | Versucht, den Gegner zum Kooperieren zu bewegen.
Ziel: R (= 3 Punkte) Gefahr: Kann ausgenutzt werden, das führt zu S (=0 Punkte) |
| aggressiv | Versucht, den Gegner zu übervorteilen. Ziel: T (= 5
Punkte) Gefahr: Gegner kann ebenfalls defektieren, das führt zu P (= 1 Punkt) |
| blind | Spielt eine feste oder zufällige Strategie |
Tabelle 5: Klassifikation von Strategien
Es existiert eine Reihe von einfachen Standardstrategien, die benutzt werden können, um neue Strategien zu testen. Im folgenden werden einige Strategien zusammen mit einer Klassifikation nach Tabelle 5 angegeben, falls eine Strategie zu zwei Gruppen zugeordnet wurde, ist die erste dominant. Die Darstellung der Strategie erfolgt dabei in Pseudocode, der z.B. einfach in Lisp-Code für die oben angesprochene Experimentierumgebung übersetzt werden kann. Die Strategien sind Mathieu/Delahaye (a) entnommen.
Robert Axelrod hat 1981 zwei Computerturniere durchgeführt, um gute, oder gar die beste Strategie zu finden. Für das erste Turnier hat er professionelle Spieltheoretiker aufgefordert, ihre Strategien zu implementieren und einzusenden. Als Modus wurde ein round-robin-Turnier veranstaltet, in dem jede Strategie einzeln jeweils 200 Züge gegen alle anderen, sich selbst und random angetreten ist. Das Turnier wurde fünf mal wiederholt, um eventuelle Einflüsse von Zufallsentscheidungen zu minimieren. Die Ergebnisse sind in Axelrod (1988) beschrieben. Die Anzahl der Züge war den Autoren der Strategien vorher nicht bekannt.
Unter den 14 Einsendungen befand sich als einfachstes Programm tit-for-tat, das Sieger des Turniers wurde. Diese Strategie war vorher bekannt und hatte in zwei vorbereitenden Turnieren sehr gut abgeschnitten, was die meisten Teilnehmern wußten. Viele der eingereichten Strategien basierten auf tit-for-tat und versuchten, die Strategie zu verbessern, was allerding keiner der Strategien gelungen ist. Dieses überraschende Ergebnis hat Axelrod veranlaßt, das Turnier in größerem Rahmen zu wiederholen. Allen Teilnehmern wurden die Ergebnisse des ersten Turniers zugänglich gemacht und es stand jedem frei, eine beliebige Strategie einzusenden, also insbesondere auch solche, die beim ersten Turnier teilgenommen haben. Unter den 62 Einsendunden der zweiten Runde befand sich aber nur einmal tit-for-tat, vom gleichen Teilnehmer wie in der ersten Runde eingereicht. Auch hier traten wieder alle Strategien gegeneinander an, die Rundenzahl wurde jedoch zufällig festgelegt und betrug im Schnitt 151 Runden. Wiederum hat tit-for-tat gewonnen. Es ist aber nicht so, daß tit-for-tat unter allen Umständen die höchste Punktzahl erringen kann, das Umfeld, d.h. die Menge der andere Strategien bestimmt den Erfolg.
Tit-for-tat muß eine Reihe von Eigenschaften besitzen, die es zu einer guten Strategie machen, die gegen verschiedenste Gegner erfolgreich ist.
Zunächst war auffällig, daß freundliche Strategien generell besser abgeschnitten haben, als unfreundliche. Freundliche Strategien sind solche, die zu Beginn kooperieren und sich allgemein kooperativ verhalten. Sie erreichen untereinander im Schnitt R=3 Punkte, unfreundliche Strategien können nur dann besser sein, wenn sie häufig T=5 Punkte erreichen. Das ist aber, wie oben argumentiert, nur gegen sehr naive Strategien möglich. Die Reihenfolge unter den freundlichen Strategien wird dadurch bestimmt, wie sie gegen unfreundliche abschneiden. Unter den unfreundlichen Strategien muß zwischen den agressiven und kooperativen unterschieden werden: Bei einer agressiven Strategie gibt es nur die Möglichkeit, ebenfalls zu defektieren, um nicht ausgebeutet zu werden, oder aus Sicht des eigenen Ergebnisses gesehen, wenigstens die Punkte für P zu bekommen. Dafür ist die Eigenschaft wichtig, zurückzuschlagen, d.h. eine Defektion nicht unbeantwortet zu lassen. Komplizierter ist die Situation bei einer unfreundlichen kooperativen Strategie als Gegner: Es ist möglich, die Strategie zum Kooperieren zu bewegen, und so R=3 Punkte zu bekommen statt P=1. Entweder versucht die Strategie selbst die Initiative zu ergreifen, und eine erneute Kooperation anzuregen und läuft dabei Gefahr, S=0 Punkte zu bekommen, oder sie wartet auf die Initiative des Gegners und entscheidet dann, ob sie sich auf einer Kooperation einlassen will, oder nicht. Tit-for-tat hat die Eigenschaft, nachgiebig zu sein, d.h. nach dem Zurückschlagen Kooperation wieder zuzulassen. Eine Strategie wie spite hat diese Eigenschaft nicht. Letztendlich gibt es noch komplexere Strategien als Gegner, die versuchen die Strategie des Gegners zu analysieren und daraufhin zu versuchen, Kooperation zu etablieren. Die Analyse der Strategie kann aber nur gelingen, wenn die Strategie einfach, d.h. ihr Verhalten für den Gegner durchschaubar ist.
Im ersten von Axelrod durchgeführten Turnier wurde die Reihenfolge unter den acht freundlichen Strategien von zwei Eigenschaften entschieden. Die erste zeigte sich im Kontakt mit einer komplexen Strategie, die die bedingten Wahrscheinlichkeiten zu berechnen versuchte, wie die gegnerische Strategie auf Defektion bzw. Kooperation reagiert. Das gelang nur bei einfachen Strategien, die damit einen Vorteil gegenüber den weniger einfach zu durchschauenden hatten. Die zweite entscheidende Eigenschaft war Nachsichtigkeit. Die am wenigsten nachsichtige Regel (äquivalent zu spite) schnitt unter den freundlichen Strategien am schlechtesten ab, die am meisten nachsichtigen, darunter tit-for-tat, am besten. Eine noch nachsichtigere Regel als tit-for-tat, tit-for-two-tats, die erst nach zwei aufeinanderfolgenden Defektionen selbst defektiert, hätte übrigens das erste Turnier gewonnen. Die vier Eigenschaften einer guten Strategie sind zusammenfassend:
Mathieu und Delahaye (a) stellen die Frage, ob eine allgemein bessere Strategie als tit-for-tat möglich ist und haben aus ihren Überlegungen heraus gradual entwickelt, eine Strategie, die beim ersten Zug kooperiert, das erste Defektieren des Gegners mit einem Defektieren und anschließend zwei Kooperationen, schließlich das n-te Defektieren des Gegners mit n Defektionen und zwei Kooperationen beantwortet. Dabei ist die von Axelrod aufgestellte Forderung nach Einfachheit verletzt, den die Strategie benötigt Wissen über das gesamte Spiel seit Beginn, tit-for-tat kommt mit dem Wissen über den letzten Zug des Gegners aus. Die Autoren identifizieren zwei herausragende Merkmale an gradual, die tit-fot-tat nicht hat, die aber in besonderer Weise natürlich seien, d.h. dem Verhalten von Menschen, Märkten, usw. näher kommen. Gradual ist sehr offensiv, indem es den Gegner zur Kooperation zwingt: Nichtkooperation zahlt sich für ihn immer weniger aus, denn sie wird mit einer immer größeren Anzahl von Defektionen beantwortet. Gleichzeitig ist die Strategie sehr defensiv und möchte nicht ausgebeutet werden, deshalb wählt sie nach Ausbeutungsversuchen immer seltener die risikoreiche Kooperation, sondern beschränkt sich häufiger auf die rationale Wahl des einfachen Gefangenendilemmas, nicht zu kooperieren. Tabelle 6 zeigt die Ergebnisse eines von Mathieu und Delahaye durchgeführten round-robin Turniers mit den oben beschriebenen Strategien und gradual.
| Strategie | Punkte |
|---|---|
| gradual | 33416 |
| tit-for-tat | 31411 |
| soft_majo | 31210 |
| spite | 30013 |
| prober | 29177 |
| pavlov | 28910 |
| mistrust | 25921 |
| cooperate | 25484 |
| per_kind | 24796 |
| defect | 24363 |
| per_nasty | 23835 |
| random | 22965 |
Tabelle 6: Ergebnis eines round-robin Turniers
In den Übungen zu "Programmieren für CL/KI I: Lisp" wurden von mir zweimal round-robin Turniere mit den von den Studenten entwickelten Strategien druchgeführt. Die Ergebnisse decken sich prinzipiell mit den hier vorgestellten, tit-for-tat und Varianten waren realtiv häufig vertreten und konnten gewinnen. Bei den abgegebenen Lösungen war häufig die Tendenz festzustellen, daß die Strategien den Gegner irgendwie "überlisten" sollten, und dadurch mehr als R=3 Punkte im Schnitt erreicht werden sollten. Es hat sich aber gezeigt, daß agressive Strategien keine besonders guten Ergebnisse erreichen. Die bei den Turnieren verwendeten Strategien finden sich bei der Experimentierumgebung in Lisp.
Die selbe Strategie kann in einem Turnier gut, in einem anderen schlecht abschneiden. Der Erfolg hängt von der Umgebung, d.h. den anderen beteiligten Strategien ab. Im direkten Vergleich mit defect ist cooperate chancenlos. Wenn sich aber eine größere Menge kooperativer Strategien am Turnier beteiligen, wird cooperate eine höhere Punktzahl erhalten, als defect, wie z.B. in Tabelle 6 zu sehen ist. Um herauszufinden, ob eine Strategie allgemein gut abschneidet, müßte eine große Anzahl von Turnieren mit wechselndem Umfeld durchgeführt werden. Dabei würden "erfolgversprechende" Strategien häufiger ausgewählt, offensichtlich erfolglose Strategien schnell aussortiert. Ein solches Verfahren erinnert an natürliche Selektion und weist in Richtung Evolution und ökologische Simulation.
Axelrod hat dementsprechend eine zweite Turnierform eingeführt, in der für Populationen von Strategien die Fitness, d.h. die Punktzahl gegen die anderen Strategien der Population, bestimmt und dann die Zusammensetzung der nächsten Generation festgelegt wird. Grundlegender Unterschied zum round-robin Turnier ist, daß eine Strategie mehrfach vertreten sein kann. Der Anteil der Instanzen einer Strategie an der Gesamtpopulation ist zu Beginn des Turniers für alle teilnehmenden Strategien gleich, nach jeder Runde wird die neue Generation so zusammengesetzt, daß der Anteil einer Strategie proportional zu ihrer erreichten Punktzahl ist. Eine Strategie, die in der Summe ihrer Instanzen doppelt soviele Punkte wie eine andere erzielt, wird also in der nächsten Generation doppelt so oft vertreten sein. Schlechte Strategien (bezogen auf das spezifische Umfeld in dieser ökologischen Simulation) werden aussterben, gute Strategien ihren Anteil erhöhen. Nach einer gewissen Anzahl Iterationen stellt sich ein stabiles Gleichgewicht der Anteile der Strategien an der Gesamtpopulation ein.
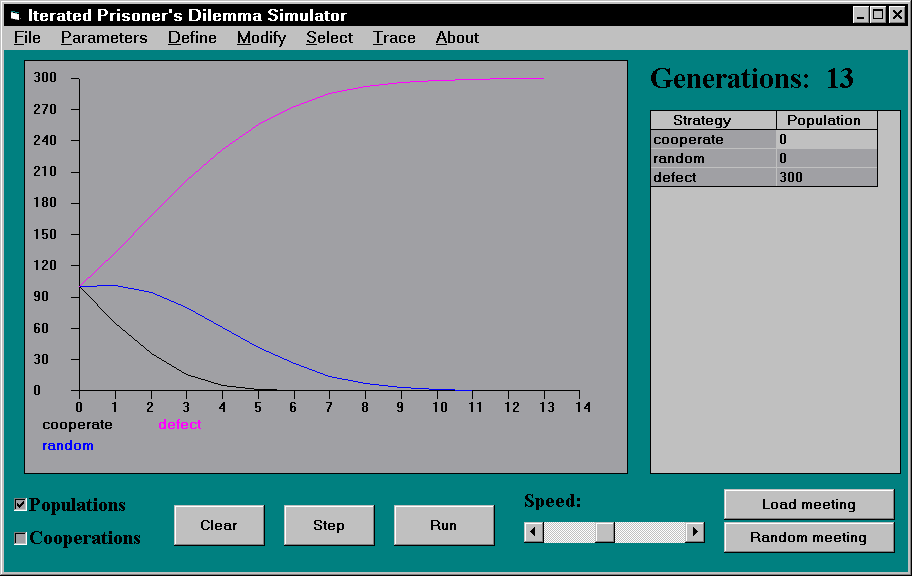
Mathieu und Delahaye haben einen "Iterated Prisoner's Dilemma Simulator" entwickelt, mit dem sich ökologische Simulationen mit verschiedenen Zusammensetzungen einfach durchführen lassen. Abbildung 1 zeigt das Ergebnis eines Laufes mit 3 verschiedenen Strategien, die zu Beginn mit jeweils 100 Instanzen vertreten waren. Eine Strategie wird "stabil" in bezug auf eine Startverteilung von Strategien genannt, wenn sie bei Erreichen eines Gleichgewichtszustandes nicht ausgestorben ist. defect ist im ersten Beispiel die einzige stabile Strategie, sowohl random als auch cooperate sterben aus. Interessant ist der Unterschied zwischen cooperate und random: Cooperate (schwarze Kurve) erzielt sowohl gegen random als auch gegen defect schlechte Resultate und stirbt daher sehr schnell aus, die Anzahl der Instanzen in der Gesamtpopulation sinkt monoton. Random (blaue Kurve) besiegt cooperate, unterliegt aber defect. Solange noch eine ausreichend große Anzahl von cooperate-Instanzen vorhanden ist, steigt die Anzahl von random-Instanzen, sobald diese aber ausgestorben, bzw. im Verhältnis zu defect zu wenige geworden sind, stirb auch random aus.

Abbildung 1: Ökologische Simulation mit 3 Strategien. (Simulator von Mathieu/Delahaye)
Aus diesem Ergebnis darf aber nicht der Schluß gezogen werden, daß cooperate generell eine schlechte und defect generell eine gute Strategie sei. Abbildung 2 und 3 zeigen die Ergebnisse umfangreicherer Simulationen, in denen cooperate eine stabile Strategie ist, defect aber nicht. In dem in Abbildung 2 dargestellten Experiment ist nur tit-for-tat zu den drei Strategien aus Abbildung 1 hinzugekommen. Das Ergebnis weicht in dramatischer Weise vom obigen ab: Zwar kann defect zu Beginn seinen Anteil erhöhen, aber mit dem Aussterben von random stirbt auch defect aus. cooperate, daß gegen defect und random sehr schlechte Resultate erzielt (im Schnitt S=0 bzw. (R=3 + S=0)/2=1.5 Punkte), erweist sich als stabil. Bestätigt wird das Ergebnis von Abbildung 3, in dem alle freundlichen Strategien stabil sind, alle unfreundlichen (inklusive mistrust, das nur eine minimale Abänderung von tit-for-tat ist) Strategien sterben aus.
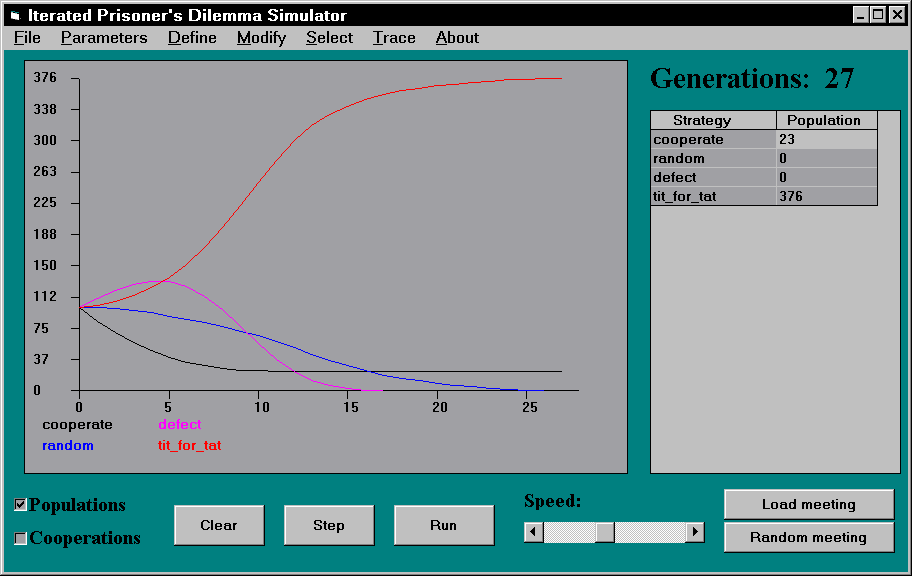
Abbildung 2: Ökologische Simulation mit 4 Strategien.
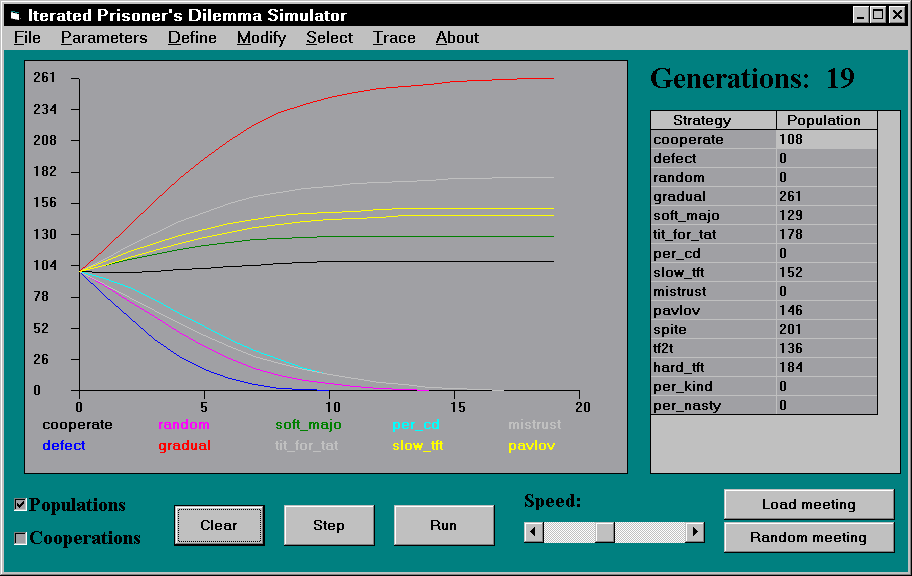
Abbildung 3: Simulation mit 15 Strategien
Aus solchen Ergebnissen heraus stellt Axelrod weitergehende Überlegungen an. Es hat sich gezeigt, daß tit-for-tat sehr erfolgreich ist, was dazu führen könnte, daß in einer ökologischen Simulation jeder diese Strategie verwendet. Kann es in einer solchen Situation lohnend sein, eine andere Strategie zu verwenden, oder anders formuliert: Kann es einer anderen Strategie gelingen, in eine Population von tit-for-tat Instanzen einzudringen? Dazu müßte sie gegen eine Instanz der vorhandenen Strategie mehr Punkte bekommen, als diese untereinander. Eine Strategie wird kollektiv stabil genannt, wenn keine andere in sie eindringen kann.
Eine Population von tit-for-tat Instanzen erhält in jedem Zusammentreffen von zwei tit-for-tat Strategien R (= Reward) Punkte, da keine von ihnen von sich aus defektiert. Eine eindringende Strategie kann nur dann mehr Punkte erhalten, wenn sie irgendwann defektiert und somit T Punkte erhält. Im Gegenzug würde wiederum tit-for-tat defektieren und den Vorteil zunichte machen. tit-for-tat ist aber nur dann kollektiv stabil, wenn das Spiel voraussichtlich lange genug dauert, um die Vergeltung wirksam werden zu lassen. Der Diskontparameter w beschreibt die Wichtigkeit der Zukunft im Verhältnis zur Gegenwart: Je weniger bedeutend die Zukunft ist, desto lohnender kann es sein, in der Gegenwart einen Gewinn zu erzielen. Wenn w groß genug ist, kann keine Strategie in eine tit-for-tat Population eindringen, Axelrod formuliert ein Theorem: (Axelrod, S.53)
Theorem 2: TIT FOR TAT ist genau dann kollektiv stabil, wenn w hinreichend groß ist. Der kritische Wert von w ist eine Funktion der vier Parameter T, R, P und S.
Es gibt aber auch Strategien, die immer kollektiv stabil sind, z.B. defect. Niemand kann gegen defect mehr als P Punkte pro Runde erreichen. Gegen einen Gegner, der immer defektiert, gibt es keinen Grund, nicht ebenfalls immer zu defektieren. Diese Überlegungen bezogen sich aber nur auf das Eindringen einer einzelnen Instanz einer Strategie in eine gesamte Population von anderen. Wenn mehrere Instanzen der gleichen Strategie einzudringen versuchen, müssen auch noch die Wechselwirkungen der eindringenden Instanzen untereinander mitberücksichtigt werden. defect-Instanzen erreichen gegeneinander immer P=1 Punkte, bei angenommenen 10 Runden des Gefangenendilemmas also 10 Punkte, tit-for-tat Instanzen erreichen gegen defect im ersten Zug S=0 Punkte, in jedem weiteren P=1, also bei 10 Runden 9 Punkte. Das ist geringfügig schlechter, als defect gegen defect, allerdings erreicht tit-for-tat, wenn es auf sich selbst trifft 10 * R= 30 Punkte. Wenn tit-for-tat einen Anteil p seiner Interaktionen mit anderen tit-for-tat Instanzen hat, ergibt sich ein Anteil von 1-p mit defect-Instanzen. Die durschnittliche Punktzahl für tit-for-tat ist also 30p+9(1-p). Wenn diese Punktzahl mehr als 10 beträgt, kann eine Gruppe von tit-for-tat Instanzen in eine Population von defect-Instanzen eindrigen. Es reicht ein Anteil von 1/21, also ca. 5% von tit-for-tat Instanzen aus, um sich gegen eine defect-Population zu behaupten.
Axelrod untersucht dann weiter, welche Auswirkungen das für die Erfolgschancen von mutierten Strategien hat, Matthieu und Delahaye (a) haben Versuche mit veränderlichen Strategien und genetischen Algorithmen durchgeführt, um optimalere Strategien zu finden.
Bisher wurde nur das klassische Gefangenendilemma betrachtet, das an die payoff-Matrix zwei Bedingungen gestellt hat:
In der Literatur zur Spieltheorie und dem Gefangenendilemma finden sich aber zahlreiche Varianten, die diese Forderungen verletzen, es scheint sogar eher die Regel zu sein, daß zunächst eine neue Variante entworfen und dann analysiert wird. An dieser Stelle wird nicht zu detailliert auf Varianten eingegangen, da die grundlegenden Konzepte und Begriffe sich nicht stark vom klassischen iterierten Gefangenendilemma unterscheiden.
Tabelle 7: payoff-Matrix für das
Leader's-Dilemma Mathieu und Delahaye (b) beschreiben das Leader's Dilemma (s.
Tabelle 7), das sich vom klassischen Gefangenendilemma dadurch
unterscheidet, daß S > R ist. Es ist also besser, sich
"ausbeuten" zu lassen, als gegenseitig zu kooperieren.
Noch besser ist es allerdings, abwechselnd T und S zu erhalten,
die Punktzahl ist dann (T+S)/2=4, bei ständiger Kooperation gibt
es nur 1 Punkt. Der Unterschied zum Lift-Dilemma (Tabelle 8) ist
nicht sehr groß, deshalb wird hier auf eine eingehende
Beschreibung möglicher erfolgreicher Strategien verzeichtet. Ein anschauliches Beispiel für das Leader's Dilemma ist
folgende Situation: Auf dem Weg durch unwegsames Gelände kommen zwei Wanderer zu
einem sehr schmalen Weg, der durch einen dichten Wald führt.
Wenn beide gleichzeitig versuchen voranzugehen, kommen sie nur
sehr schlecht vorwärts (R=1 Punkt), wenn keiner von beiden geht,
gelangen sie nicht ans Ziel (P=0). Wenn einer vorangeht und der
andere hinterher, gelangen beide relativ schnell durch den Wald,
der vordere hat allerdings weniger Probleme, weil der
Nachfolgende mit zurückschlagenden Ästen usw. zu kämpfen hat. Tabelle 8: payoff-Matrix für das
Leader's-Dilemma Als ein Beispiel für eine Variante, die komplexe
Strategien nötig macht, untersuchen Mathieu und Delahaye (c,d)
das Lift-Dilemma, bei dem die Forderung (T+S)/2 < R verletzt
ist. Es sind zwei Ebenen von Kooperation möglich: Um die zweite Ebene der Kooperation zu erreichen, ist
Meta-Kooperation nötig, d.h. eine Abstimmung darüber, wer
zuerst kooperiert und dann defektiert. Mathieu und Delahaye geben
einige Situationen an, die durch das Lift-Dilemma beschrieben
werden können: Wie kann so eine kompliziertere Kooperation erreicht werden?
Keine deterministische Strategie kann gegen sich selbst eine
Ebene-2 Kooperation etablieren, denn eine Kommunikation zwischen
den Gegnern über die reinen Spielzüge hinaus ist nicht
möglich. Es müßte eine Verständigung darüber stattfinden,
wer zuerst defektiert, also den Gegner ausbeutet. Zwei Instanzen
einer deterministischen Strategie verhalten sich gegeneinander
aber völlig identisch, also können sie nicht "außer
Phase" geraten, d.h. eine deterministische Strategie spielt
gegen sich selbst nie [c,d] oder [d,c]. Deshalb haben Mathieu und
Delahaye das nichtdeterministische, probabilistische reason entwickelt,
das folgende Strategie verfolgt: Der Nachteil von reason ist, daß es zwar gegen sich selbst
die maximale Punktzahl ((T+S)/2=4) erreicht, allerdings z.B.
gegen defect chancenlos ist. Eine Verbesserung bringt die
Kombination von reason und tit-for-tat: Verbesserung: reason-tit-for-tat Die Kooperationswahrscheinlichkeit pc=0.56696 leitet sich aus
der Überlegung ab, daß eine Wahrscheinlichkeit von p=0.5 zwar
am schnellsten zu der angestrebten Ebene-2 Kooperation führt,
aber in den Runden, in denen die beiden Gegner "in
Phase" sind, nur (R+P)/2=2 Punkte erreicht werden. Mit
p=0.75 wären es z.B. 0.75*3+0.25*1=2.5 Punkte. Der Wert
pc=0.56696 ist das Resultat der Optimierung eines Polynoms, das
diese beiden entgegenstehenden Ziele ausdrückt: -(1 - 2pc + 2pc^2)(pc(R - P) + P - (T + S) / 2) / (2pc(1 -
pc)), mit den vorliegenden Werten R, P, T und S: -(2pc - 3)(1 - 2pc + 2pc^2) / 2pc(1 - pc) Der sich ergebende Wert von pc=0.56696 weicht nur geringfügig
von 0.5 ab, der Gewinn liegt bei weniger als 1/10 Punkt. Für
eine genaue Herleitung von pc siehe Mathieu und Delahaye (c). Bei der Betrachtung realer Situationen stellt das klassische
iterierte Gefangenendilemma natürlich nur eine grobe
Abstrahierung dar, dasselbe gilt für die vorgestellten
Varianten. Es gibt eine Reihe von Ansätzen, die neue Qualitäten
zu den Modellen hinzufügen. Zum einen ist dies das Vorhandensein
von Rauschen und Unsicherheit: In den bisher betrachteten
Situationen konnte eine Strategie sicher sein, daß der von ihr
beobachtete Zug des Gegners auch tatsächlich derjenige war, den
die andere Strategie ausgeführt hat. Um mit solcher Unsicherheit
umzugehen, müssen die Strategien toleranter sein, spite z.B.
hätte bei möglichen falschen Übermittlungen von Zügen in
einer ökologischen Simulation keine Chance, stabil zu sein.
Grundsätzlich ist die Einführung von probalistischen Strategien
notwendig, um mit bekannten oder unbekannten Unsicherheiten
zurecht zu kommen. In den bisher betrachteten Modellen gibt es nur zwei
Möglichkeiten: kooperieren oder defektieren. In realen
Situationen haben beide Gegner aber zusätzlich die Möglichkeit
auszusteigen, d.h. das Spiel zu beenden. Das hat auch
Auswirkungen auf den Diskontparameter w, der bei der Definition
kollektiv stabiler Strategien die relative Wichtigkeit der
Zukunft beschrieben hat. Es könnte dann z.B. die Forderung
aufgestellt werden, daß sich ein Individuum, d.h. eine Instanz
eine Strategie nicht vollständig aus allen Interaktionen
zurückziehen kann, sondern eine gewisse Anzahl Partner wählen
muß. Als letzen Punkt möchte ich noch die Erweiterung der
Kommunikationsmöglichkeiten ansprechen: Die dargestellte
Situation, in der die Gegner keine anderen Informationen als die
Züge des Gegenübers erhalten können, mußte künstlich
hergestellt werden. Realistischer sind eine ganze Reihe von
zusätzlichen Informationskanälen, die allerdings nicht
zuverlässig sein müssen, d.h. Selbstaussagen einer Strategie
über sich selbst können falsch, also gelogen sein. Bei den
Lispstrategien, die die Erstsemester in den Übungen zu
"Programmieren für CL/KI I" erstellt haben, wurde
mehrfach der Versuch unternommen, zu betrügen, z.B. indem
globale Variablen oder Definitionen geändert wurden, um dem
Gegner eine veränderte Situation unterzuschieben. Die Versuchung
der Spielmanipulation auf einer Meta-Ebene ist also vorhanden und
muß bei komplexen Modellen mit berücksichtigt werden. Die Betrachtung möglichst einfacher, isolierter Modelle wie
dem iterierten Gefangenendilemma ist aber in vielen Fällen
komplexen, realitätsnäheren Modellen vorzuziehen, weil nur so
die relevanten Parameter und wichtigen Eigenschaften von
Strategien isoliert und untersucht werden können. Das Gefangenendilemma zeigt Verhaltensstrategien für das
Überleben "in der Wildnis", d.h. einer Welt, in der
sich nicht alle Agenten freundlich gesonnen sind und notwendig
kooperieren. Dabei entstehende Konflikte können auf Konflikte
zwischen einfachen Strategien zurückgeführt werden und es
können grundsätzliche Untersuchungen über erfolgreiche, d.h.
konfliktlösende oder -vermeidende Strategien durchgeführt
werden. Die Anwendungsgebiete des Erklärungsmodells
"Gefangenendilemma" und seiner Varianten sind sehr
breit gefächert: Überall, wo handelnde Individuen (oder als ein
Individuum zu betrachtende Gruppen) mit potentiell
konfligierenden Zielen aufeinandertreffen, müssen sie eine
Strategie wählen, um ihr Ziel zu erreichen. Viele biologische,
wirtschaftswissenschaftliche oder soziologische Vorgänge können
mit Varianten des Gefangenendilemmas erklärt werden: Es ist
damit ein mögliches Modell für die Erforschung von Artificial
life. Axelrod, R. (1988): Die Evolution der Kooperation, München:
Oldenbourg Hofstadter, D. (1991): Metamagicum, Stuttgart: Klett-Cotta Mathieu, P.; Delahaye, J.P. (a): Our meeting with gradual: A
good strategy for the iterated prisoner's dilemma Mathieu, P.; Delahaye, J.P. (b): Complex strategies in the
iterated prisoner's dilemma Mathieu, P.; Delahaye, J.P. (c): The iterated lift dilemma Mathieu, P.; Delahaye, J.P. (d): Random strategies in a two
level iterated prisoner's dilemma: How to avoid conflicts? McCain, R.A.: Game theory - An introductionary sketch, http://wiliam-king.www.drexel.edu/top/eco/game/game.html Von Tobias Thelen, 1998-20004.1. Das Leader's-Dilemma
A / B
cooperate
defect
cooperate
R=(1,1)
S=(3,5)
defect
T=(5,3)
P=(0,0)
4.2. Das Lift-Dilemma
A / B
cooperate
defect
cooperate
R=(3,3)
S=(0,8)
defect
T=(8,0)
P=(1,1)
Zwei Nachbarn hören gerne laut Musik und können in
ihrem Genuß durch die Musik des anderen gestört werden,
es gibt folgende Möglichkeiten:
[c,d]: Ich höre meine Musik, der Nachbar ist still, das
bringt mir 8 "Genußpunkte".
[d,c]: Der Nachbar hört seine Musik, ich bin still. Das
bringt mir keine "Genußpunkte".
[d,d]: Ich höre meine Musik, werde aber durch die des
Nachbarn gestört: 1 "Genußpunkt".
[c,c]: Keiner von beiden hört Musik, die Stille bringt 3
"Genußpunkte".
Diese Situation ist eine Generalisierung der vorigen, zu
kooperieren bedeutet den Versuch, Zugriff zu erlangen und
dabei die Fairness, oder Absprachen zu berücksichtigen.
Zu defektieren bedeutet den Versuch, Zugriff ohne
Rücksicht zu erlangen. Eine [d,c] Runde stellt dann das
Unterordnen des zweiten Spielers unter die Dominaz des
ersten dar. In der Tierwelt ist häufig zu beobachten,
daß Kämpfe nicht bis "auf Blut" ausgefochten
werden, sondern nur bis einer der Opponenten aufgibt und
seine Unterordnung signalisiert. Dadurch gewinnen beide,
der Überlegene allerdings mehr als der Unterlegene.
4.3. Weitere Varianten
5. Ausblick
Literatur:
Experimentierumgebung in Lisp
;;; -------------------------------------------------
;;; -------------------------------------------------
;;;
;;; deal.lsp
;;; Tobias Thelen
;;; 13.11.1997
;;;
;;; Beispiel Spieltheorie nach:
;;; Hofstatter, Douglas R.: Metamagicum
;;;
;;; getestet:
;;; Allegro CL
;;; CLISP
;;; G_LISP
;;;
;;;
;;; Zwei 'Spieler' treten gegeneinander an:
;;; Der eine hinterlegt Geld, der andere Diamanten
;;; beide wissen voneinander nicht, ob sie wirklich die
;;; Gegenleistung erhalten. Das Spiel wird mehrmals wieder-
;;; holt, so dass sich das eigene fruehere Verhalten auf
;;; das zuknftige des Gegners auswirken kann.
;;;
;;; -------------------------------------------------
;;
;; deal-shell (Funktion-1 Funktion-2 Iterationen)
;;
;; Aufruf der Funktion:
;;
;; (deal-shell Funktionsname1 Funktionsname2 Anzahl-Runden)
;;
;; Beispiel:
;; (deal-shell 'again 'a-total 100)
;; oder:
;; (deal-shell #'again #'a-total 100)
;;
;; Liefert eine Cons-Zelle, die die Anzahl der Punkte
;; fuer die erste und zweite Funktion enthaelt.
;;
;; Beispiel:
;;
;; (200.229)
;; Die erste Funktion hat 200 Punkte bekommen
;; Die zweite Funktion hat 229 Punkte bekommen
;;
(defun deal-shell (fct-1 fct-2 times)
(setq *moves* '())
(let ((p1 0) (p2 0))
(dotimes (i times)
(let* ((r1 (funcall fct-1 (beginner) (follower)))
(r2 (funcall fct-2 (follower) (beginner)))
(res (gewinnmatrix r1 r2)))
(setq p1 (+ p1 (car res)))
(setq p2 (+ p2 (cdr res)))
(setq *moves* (cons (cons r1 r2) *moves*))))
(cons p1 p2)))
;;
;; gewinnmatrix (zug-a zug-b)
;; return Cons-Zelle (+-a,+-b)
;;
(defun gewinnmatrix (a b)
(cond ((not (or a b)) '(1 . 1))
((and a (not b)) '(0 . 5))
((and b (not a)) '(5 . 0))
((and a b) '(3 . 3))))
;;
;;
;; beginner
;; Zugriffsfunktion auf letzten Zug des ersten Spielers
;;
(defun beginner ()
(if (null *moves*) nil (caar *moves*)))
;;
;; follower
;; Zugriffsfunktion auf letzten Zug des zweiten Spielers
;;
(defun follower ()
(if (null *moves*) nil (cdar *moves*)))
;;; ---------------------------------------------------
;;
;; Beispielfunktionen
;;
;;
(defun again (my-last his-last)
(cond ((null *moves*) T)
((eq my-last T) nil)
(T T)))
(defun a-total (my-last his-last)
nil)
(defun zufall (my-last his-last)
(> (random 100) 50))
(defun unbesiegbar (my-last his-last)
(cond ((null *moves*)
(setq *unbesiegbar-truhe* 0)
(setq *unbesiegbar-strategie* T)
T)
((not *unbesiegbar-strategie*) nil)
((eq his-last nil)
(setq *unbesiegbar-truhe* (1+ *unbesiegbar-truhe*))
(if (> *unbesiegbar-truhe* 2)
(setq *unbesiegbar-strategie* nil)
T))
(T T)))
(defun tft (mylast opplast)
(if (null *moves*) T opplast))
;; -------------------------------------------------------------
;; Thomas Klein und Sebastian Misch
(defun ALWAYS-ULTRA-SADISTIC (mylast hislast) "Thomas Klein & Sebastian Misch" ;; Oben genannte Funktion 8-)
(if (null *moves*) ;; Wenn erster Durchlauf...
(let () (setq *hisstrategy* ()) ;; Seine Strategieliste
(setq *fatstrategy* ()) ;; Unsere Strategieliste
(setq *myNIL* NIL) ;; UNSER Special Agent Nil
(setq *is_atotal* T) ;; Ist der Gegner A-Total-like
(defun lastlast(liste) ;; Gibt Element[n-2] zurueck
(nth (- (length *moves*) 1) liste) ;;
) ;;
;(defun NIL () T) ;; no comment 8>
;(defun T () *myNIL*) ;; no comment 8>
;(defun random (x) ; Um Zufallsfunktion random zu manipulieren... ;-)
; 100 ; Und schon kooperiert die Zufalls-Funktion.
;) ; Wenn das erlaubt ist, dann bitte auskommentieren
) ; Wir wissen, dass das unfair waere...
*myNIL*
)
(setq *hisstrategy* (append *hisstrategy* (list hislast)));; Sein Verhalten mitloggen ;->
(setq *fatstrategy* (append *fatstrategy* (list mylast))) ;; Auch unseres....
(dolist (n *hisstrategy* *myNIL*) ;; Seine Strategie auf Haeufigkeit
(if n (setq *is_atotal* *myNIL*)) ;; von NIL pruefen.
) ;; Nur NILs -> IS_ATOTAL
(if *is_atotal* *myNIL* ;; ATOTAL? Dann nur NILlen
(if (null *moves*) *myNIL* ;; Schlechten Eindruck schinden...
(cond ;; Fallunterscheidung
((AND (lastlast *hisstrategy*)
(lastlast *fatstrategy*))
(if (not hislast) *myNIL* T)
) ; (1 & 1) (0 -> 0 / 1 -> 0)
((AND (lastlast *hisstrategy*)
(NOT (lastlast *fatstrategy*)))
(if (not hislast) *myNIL* T)
) ; (1 & 0) (0 -> 0 / 1 -> 0)
((AND (NOT (lastlast *hisstrategy*))
(lastlast *fatstrategy*))
(if (not hislast) *myNIL* *myNIL*)
) ; (0 & 1) (0 -> 0 / 1 -> 0)
((AND (NOT (lastlast *hisstrategy*))
(NOT (lastlast *fatstrategy*)))
(if (not hislast) T *myNIL*)
) ; (0 & 0) (0 -> 0 / 1 -> 0)
)
)
)
)
; ------------------------------------------------------------------------
; Torsten Bunde
(defun tbunde (My-Last His-Last) "Torsten Bunde"
(if his-last
(let () ; Wenn Gegner gesetzt hat
(setq *tbundeGesetzt* (1+ *tbundeGesetzt*))
(setq *tbundeNHintereinander* 0)
(setq *tbundeHintereinander* (1+ *tbundeHintereinander*))
)
(let () ; Wenn Gegner nicht gesetzt hat
(setq *tbundeNGesetzt* (1+ *tbundeNGesetzt*))
(setq *tbundeNHintereinander* (1+ *tbundeNHintereinander*))
(setq *tbundeHintereinander* 0)
) )
(if (not *tbundeStrategie*) ; Wenn Strategie = false, dann
nil ; nil
(cond ((Null *moves*) ; sonst
(setq *tbundeGesetzt* 1)
(setq *tbundeNGesetzt* 1)
(Setq *tbundeNHintereinander* 0)
T
)
((> *tbundeHintereinander* 3) (setq *tbundeStrategie* nil)
(setq *tbundeHintereinander* 0)
nil)
((> *tbundeNHintereinander* 1)(setq *tbundeStrategie* nil)
nil)
((>= (/ *tbundeGesetzt* *tbundeNGesetzt*) 1)
(setq *tbundeStrategie* T)
T)
(T nil)
) ))
(setf *tbundeStrategie* nil) ; Strategievariable, entscheidet ob gesetzt
; wird oder nicht.
(setf *tbundeGesetzt* 0) ; Anzahl, wie oft Gegner gesetzt hat
(setf *tbundeNGesetzt* 0) ; Anzahl, wie oft er nicht gesetzt hat
(setf *tbundeNHintereinander* 0) ; Anzahl, wie oft er hintereinander gesetzt
; hat
(setf *tbundeHintereinander* 0) ; Anzahl, wie oft er hintereinander nicht
; gesetzt hat
; Diese Funktion arbeitet nach folgendem Prinzip. Hat mein Gegner zweimal
; hintereinander nichts gesetzt, so setze ich solange nichts mehr, bis er
; wieder einmal gesetzt hat. Hat er wieder gesetzt, setze ich wieder solange,
; bis er zweimal hintereinander nichts gesetzt hat! Hat er dagegen mehr als
; dreimal hintereinander gesetzt, setze ich nichts mehr. Wenn das Verhaeltnis
; von Gesetzt zu Nichtgesetzt groesser ist als 1 fange ich wieder an zu setzen,
; da der Gegner "glaubwrdig" erscheint!
(defun tbunde2 (My-Last His-Last)
(if (not (null *moves*))
(if his-last
(setq *tbunde2set* (1+ *tbunde2set*)
*tbunde2Nrep* 0
*tbunde2Rep* (1+ *tbunde2Rep*))
(setq *tbunde2Nset* (1+ *tbunde2Nset*)
*tbunde2Nrep* (1+ *tbunde2Nrep*)
*tbunde2Rep* 0)))
(cond ((null *moves*) (setq *tbunde2set* 1 *tbunde2Nset* 1 *tbunde2Nrep* 0
*tbunde2Strat* T *tbundeRep* 0) T)
((>= (/ *tbunde2set* *tbunde2Nset*) 1) (setq *tbunde2Strat* T))
((not *tbundeStrategie*) nil) ; Wenn Strategie = false, dann nil
((> *tbundeRep* 3) (setq *tbunde2Strat* nil *tbundeRep* 0) nil)
((> *tbundeNrep* 1)(setq *tbundeStrat* nil))
(T nil)))
; ------------------------------------------------------------
; Axel Doerfler
(defun anti-unbesiegbar "Axel Doerfler" (my-last his-last)
(cond (*moves* (incf *bsb-count*)
(if (> *bsb-count* 2) T nil))
(T (setq *bsb-count* 0))))
(defun his-last "Axel Doerfler" (my-last his-last)
his-last)
setq *schizo-count* 0)
(defun schizophren "Axel Doerfler" (my-last his-last)
(cond ((null *moves*)
(incf *schizo-count*)
(if (eq (mod *schizo-count* 2) 0) (setq *schi-schizo* T)
(setq *schi-schizo* nil)))
(T (setq *schizo-count* 0)))
(if *schi-schizo* (not his-last)
nil))
(let ((*killer-count* 0)(*killers* 0)(*schummel* nil))
(defun killer "Axel Doerfler" (my-last his-last)
(cond ((null *moves*) (incf *killer-count*)
(setq *killers* 0)
(if (eq (mod *killer-count* 2) 0) (setq *schummel* T)
(setq *schummel* nil)))
(T (setq *killer-count* 0)))
(incf *killers*)
(if *schummel* (if (eq *killers* 4) nil (not his-last))
(if (null *moves*) T his-last)))
)
; --------------------------------------------------------------------
; Andreas Nie
(defun past "Andreas Nie" (my his)
(cond ((null *moves*) nil)
((eq my his) my)
(T (not my))))
(defun anie-strat2 (my his)
(cond ((null *moves*) (setq *a-* nil)
(setq *a+* nil)
(setq *az* 0)
(setq *heinrich* 0)
(setq *azs* nil)
(setq *atotal* 0)
nil)
((eq *heinrich* 1) (cond ((not his) (let ()
(setq *heinrich* 0)
nil))
(T T)
))
((eq *atotal* 2) nil)
(*azs* nil)
((not his)(let ()
(setq *atotal* (1+ *atotal*))
(setq *heinrich* (1+ *heinrich*))
(setq *a-* T)
(cond ((eq *az* 3) (let ()
(setq *azs* T)
T))
((if (eq *a-* *a+*) (let ()
(setq *a-* nil)
(setq *a+* nil)
(setq *az* (1+ *az*))
T)))
(T nil))))
(T (let ()
(setq *a+* T)
(setq *atotal* 0)
(cond ((eq *az* 3) (let ()
(setq *azs* T)
T))
((if (eq *a-* *a+*) (let ()
(setq *a-* nil)
(setq *a+* nil)
(setq *az* (1+ *az*))
T)))
(T (let ()
(setq *heinrich* (1+ *heinrich*))
nil))
)
)
(defun anie-strat3 (my his)
(cond ((null *moves*) (setq *a-3* nil)
(setq *a+3* nil)
(setq *az3* 0)
(setq *heinrich3* 0)
(setq *azs3* nil)
(setq *atotal3* 0)
T)
((eq *heinrich3* 2) (cond ((not his) (let ()
(setq *heinrich3* 0)
nil))
(T T)
))
((eq *atotal3* 2) nil)
(*azs3* nil)
((not his)(let ()
(setq *atotal3* (1+ *atotal3*))
(setq *heinrich3* (1+ *heinrich3*))
(setq *a-3* T)
(cond ((eq *az3* 3) (let ()
(setq *azs3* T)
T))
((if (eq *a-3* *a+3*) (let ()
(setq *a-3* nil)
(setq *a+3* nil)
(setq *az3* (1+ *az3*))
T)))
(T nil))))
(T (let ()
(setq *a+3* T)
(setq *atotal3* 0)
(cond ((eq *az3* 3) (let ()
(setq *azs3* T)
T))
((if (eq *a-3* *a+3*) (let ()
(setq *a-3* nil)
(setq *a+3* nil)
(setq *az3* (1+ *az3*))
T)))
(T (let ()
(setq *heinrich3* (1+ *heinrich3*))
nil))
)
(defun anie-strat4 (my his)
(cond ((null *moves*) (setq *a-4* nil)
(setq *a+4* nil)
(setq *az4* 0)
(setq *heinrich4* 0)
(setq *azs4* nil)
(setq *atotal4* 0)
; T)
(if(> (+ (random 30)(random 60)) 50) T
(let ()
(setq *heinrich4* (1+ *heinrich4*))
nil)))
((eq *heinrich4* 2) (cond ((not his) (let ()
(setq *heinrich4* 1)
nil))
(T T)
))
((eq *atotal4* 3) (cond (his (let ()
(setq *atotal4* 1))
nil)
(T nil)))
(*azs4* nil)
((not his)(let ()
(setq *atotal4* (1+ *atotal4*))
(setq *heinrich4* (1+ *heinrich4*))
(setq *a-4* T)
(cond ((eq *az4* 3) (let ()
(setq *azs4* T)
T))
((if (eq *a-4* *a+4*) (let ()
(setq *a-4* nil)
(setq *a+4* nil)
(setq *az4* (1+ *az4*))
T)))
(T nil))))
(T (let ()
(setq *a+4* T)
(setq *atotal4* 0)
(cond ((eq *az4* 3) (let ()
(setq *azs4* T)
T))
((if (eq *a-4* *a+4*) (let ()
(setq *a-4* nil)
(setq *a+4* nil)
(setq *az4* (1+ *az4*))
T)))
(T (let ()
(if (> (+ (random 90) (random 50)) 20)T
(let ()
(setq *heinrich4* (1+ *heinrich4*))
nil))))
))
)
))
; ------------------------------------------------------------------------
; Britta Koch
(defun brittas "Britta Koch" (my-last her-last)
(cond ((null *moves*)
(setq *limit1* 0)
(setq *limit2* 0)
(setq *beleidigt* nil)
T)
(*beleidigt*
(if (eq her-last nil)
nil
(cond ((> *limit2* 1)
(setq *beleidigt* nil)
(setq *limit2* 0)
(setq *limit1* 0)
T
)
(T (setq *limit2* (1+ *limit2*)))
) ) )
((eq her-last nil)
(setq *limit1* (1+ *limit1*))
(if (> *limit1* 1)
(setq *beleidigt* T)
T))
(T T)
))
; ---------------------------------------------------------------------
; Collin Rogowski
(defun collins (my-last her-last)
(cond ((null *moves*) T)
((eq *davor* 1) (setq *davor* (1+ *davor*)) T)
((eq her-last T)
(setq *davor* 1) T)
(T (setq *davor* (- *davor* 1)) nil)
) )
; -----------------------------------------------------------------------
; JP Reuter
(defun jpreuterlieb "Jan Philip Reuter" (my-last his-last) T); aus ethischen Gruenden zu
; befuerworten, man stirbt aber
; vermutlich...
(defun jpreuterbelohnung "Jan Philip Reuter" (my-last his-last)
(if (equal his-last T) T nil))
; -----------------------------------------------------------------------
; Marco Diedrich
(defun MDiedrich (My-Last His-Last)
(if his-last
(setq *MdiedrichGesetzt* (1+ *MdiedrichGesetzt*)
*MdiedrichNHintereinander* 0
*MdiedrichHintereinander* (1+ *MdiedrichHintereinander*))
(setq *MdiedrichNGesetzt* (1+ *MdiedrichNGesetzt*)
*MdiedrichNHintereinander* (1+ *MdiedrichNHintereinander*)
*MdiedrichHintereinander* 0))
(if (not *mdiedrichstrat*)
Nil
(cond ((Null *moves*)
(setq *MdiedrichGesetzt* 1 *MdiedrichNGesetzt* 1
*MdiedrichNHintereinander* 0)
T)
((> *MdiedrichHintereinander* 3)
(setq *MDiedrichStrat* NIL)
(setq *MDiedrichHintereinander* 0)
Nil)
((> *MdiedrichNHintereinander* 1)
(setq *MDiedrichStrat* NIL)
Nil)
((>= (/ *MdiedrichGesetzt* *MdiedrichNGesetzt*) 5/10)
(setq *MDiedrichStrat* T)
T)
(T Nil))))
(setf *MDiedrichStrat* Nil)
(setf *MdiedrichGesetzt* 0)
(setf *MdiedrichNGesetzt* 0)
(setf *MdiedrichNHintereinander* 0)
(setf *MdiedrichHintereinander* 0)
; -------------------------------------------------------------
; Jahn-Takeshi Saito
(defun genervt "Jahn-Takeshi Saito" (my-last his-last)
his-last
)
; ------------------------------------------------------------
; Joachim Wagner
(defun jwr.get5 (my-last his-last) "eine Spieler-Funktion fuer deal.lsp"
(cond ((null *moves*) (let ()
(setq *jwr.get5.kom* 0)
(jwr.zufall 50)))
(T (let ()
(setq *jwr.get5.kom* ; Flaggen-Zustand wechseln
(+ 1 *jwr.get5.kom*))
(if (= *jwr.get5.kom* 2)
(setq *jwr.get5.kom* 0))
(if (= *jwr.get5.kom* 0) ; spielt gegen sich selbst als zweites
T ; erste Instanz beschenken
nil)))))
(defun jwr.zufall (prozent) "gibt mit prozent% Wahrscheinlichkeit T"
(< (random 100) prozent)
)
(defun jwr.get5exp (my-last his-last) "eine Spieler-Funktion fuer deal.lsp"
(cond ((null *moves*) (let ()
(setq *jwr.get5.kom* 0) ; ohne exp, damit beide Versionen zusammenarbeiten
nil))
(T (let ()
(setq *jwr.get5.kom* ; Flaggen-Zustand wechseln
(+ 1 *jwr.get5.kom*))
(if (= *jwr.get5.kom* 2)
(setq *jwr.get5.kom* 0))
(cond ((EQUAL my-last his-last) ; Gegner ist nicht jwr.get5exp (oder jwr.get5)
(jwr.zufall 50)) ; andere Strategie verwenden
((= *jwr.get5.kom* 0) ; spielt gegen sich selbst als zweites
T) ; zweite Instanz beschenkt die erste I.
(T nil)))))) ; als erste Instanz immer betruegen
(defun jwr.kill (my-last his-last) "eine Spieler-Funktion fuer deal.lsp"
(cond ((null *moves*) ; Initialisierung
T) ; mit T starten
(T (jwr.zufall 4)))) ; mit nil beantworten (4% fuer T)
(defun jwr.record (a-list a-last) "zeichnet einen Zug auf"
(cons a-last a-list)
)
(defun jwr.countT(a-list num) "zaehlt T der letzten num Zuege"
(cond ((= num 0) 0)
((null a-list) 0) ; zu wenig Zuege in der Liste
(T (+ (jwr.countT (cdr a-list) (- num 1)) ; Rest zaehlen
(if (car a-list) 1 0))))) ; Eins dazu, wenn T
; jwr.naive
;
; simuliert einen naiven Tauschpartner
(defun jwr.naive (my-last his-last) "eine Spieler-Funktion fuer deal.lsp"
(cond ((null *moves*) (let () ; Initialisierung
(setq *jwr.naive.my-moves* nil)
(setq *jwr.naive.his-moves* nil)
T)) ; mit T starten
(T (let (mv1-3 mv4-6 mv1-6 his1-6) ; Entscheidung treffen:
(setq *jwr.naive.my-moves*
(jwr.record *jwr.naive.my-moves* my-last)) ; 1. Aufzeichnen
(setq *jwr.naive.his-moves*
(jwr.record *jwr.naive.his-moves* his-last))
(setq mv1-3 (- (jwr.countT *jwr.naive.my-moves* 3) ; 2. Kooperationsver-
(jwr.countT *jwr.naive.his-moves* 3))) ; haeltnis bestimmen der
(setq mv1-6 (- (jwr.countT *jwr.naive.my-moves* 6) ; letzten Zuege 1-3, 1-6 und 4-6
(setq his1-6 (jwr.countT
*jwr.naive.his-moves* 6))))
(setq mv4-6 (- mv1-6 mv1-3)) ; (m6-m3)-(h6-h3)=(m6-h6)-(m3-h3)
(cond ((= his1-6 0) (jwr.zufall 4)) ; 6x nil mit nil beantworten (4% fuer T)
((and (> his1-6 4) (> mv1-3 -1)) ; kooperativen Partner betruegen, wenn
nil) ; nicht gerade schon getan, ggf. 2x
((> mv1-3 mv4-6) T) ; Gegener zur Kooperation motivieren, wenn Ver-
; haelnis abfaellt
((> mv1-6 3) nil) ; Zwar verbessert sich die Lage, aber der Gegner
; betruegt viel haeufiger als ich -> Kooperation lohnt nicht
; *** hier koennte man noch weitergruebeln ***
(T (jwr.zufall 50))))))) ; unentschlossen -> Muenze werfen
(setq *jwr.refined.verdacht* 'a-total)
nil))
((= (+ 1 his-nil) my-nil) (let ()
(setq *jwr.refined.verdacht* 'again)
(setq *jwr.refined.gerade* 0)
nil))
(T (let ()
(setq *jwr.refined.verdacht* 'sonst)
(jwr.naive_gate my-last his-last
*jwr.refined.my-moves*
*jwr.refined.his-moves*)))))
((equal *jwr.refined.verdacht* 'a-total)
(cond (his-last (let ()
(setq *jwr.refined.verdacht* 'sonst)
(jwr.naive_gate my-last his-last
*jwr.refined.my-moves*
*jwr.refined.his-moves*)))
(T nil)))
((equal *jwr.refined.verdacht* 'again)
(let ()
(setq *jwr.refined.gerade* (if (= 0 *jwr.refined.gerade*) 1 0))
(if (= *jwr.refined.gerade* (if his-last 1 0))
nil ; weiterhin again-Verdacht
(let () ; Verdacht verwerfen
(setq *jwr.refined.verdacht* 'sonst)
(jwr.naive_gate my-last his-last
*jwr.refined.my-moves*
*jwr.refined.his-moves*)))))
(T (if (jwr.verteilung-zufaellig *jwr.refined.his-moves*)
nil ; zufall mit nil bekaempfen
(let () ; Gegner nicht identifiziert -> naive_gate
(setq *jwr.refined.verdacht* 'sonst)
(jwr.naive_gate my-last his-last
*jwr.refined.my-moves*
*jwr.refined.his-moves*)))))))))